Blog

The Ideas Behind Things

Laura Domenech

23 Mar 2025 — 5 min read

I’ve been pondering a slippery question for some time now: What exists before a thing becomes a thing? It arose one quiet afternoon as I reflected on *information structures*. In physics we can sometimes hear that information precedes matter and form, or in the language of the dauntless physicist David Bohm, that an implicate order underlies our familiar, explicit material world. Perhaps there is some deeper layer from which reality “unfolds”. There’s a certain continuity to all this, a sense that “something” is there before we associate a form to it.

Picasso’s Bull: Distilling the Essential Line

One way to visualize this “something-before-the-thing” is a powerful illustration coming from Pablo Picasso, who famously created a series of lithographs known as “The Bull.” He began with a fairly detailed representation of a bull, then in each subsequent iteration he removed details, simplifying the image until all that remained was a few smooth essential lines. Yet somehow, those few lines are unquestionably still a bull—but in its purest, bare sense.

It’s almost as if Picasso was performing a kind of eidetic reduction—a concept introduced by philosopher Edmund Husserl (1859–1938). For Husserl, an eidetic reduction involves “peeling away” the contingencies of experience—things like specific size, color, texture—until you reach the eidos or pure essence of a phenomenon. In the bull’s case, that essence is retained even when nearly all the original details are gone.

Husserl’s Phenomenological Essence: The “Idea”

Husserl founded phenomenology with the aim of investigating consciousness and the structures of experience in a rigorous, scientific way. He argued that our everyday perception is cluttered with assumptions, memories, and expectations. By momentarily pausing these contextual preconceptions, we can slowly uncover the “idea” (eidos, essence) behind what we experience.

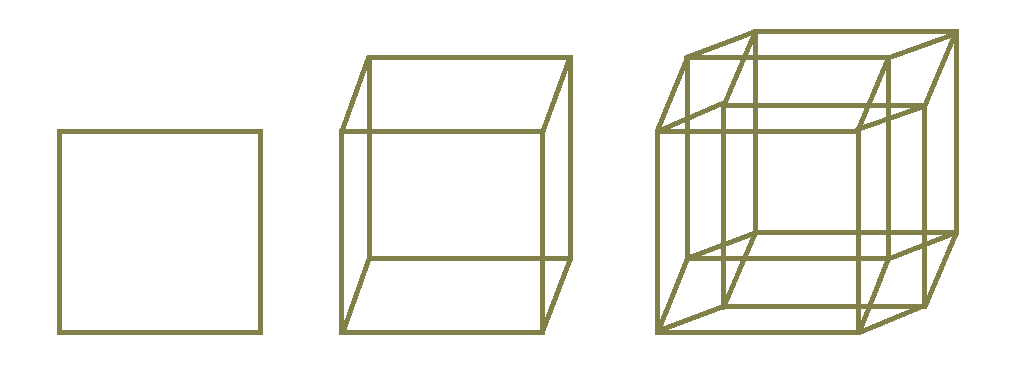
One example I often think about is about shapes. Consider the idea of a square, an instance of “squareness”. Then extending this to higher dimensions, move on to a cube, and then again to a tesseract (the four-dimensional analogue of a cube). All are variations, different “unfoldings”, of what seems to be an underlying idea. They share an eidetic core of relational structure.

From Archetypes to Category Theory

Moving from phenomenology to structural approaches. In Plato’s world, forms themselves were the ultimate realities—perfect “ideas” that our everyday objects can only approximate. Carl Jung took the concept of archetypes into psychology: universal patterns that shape the human psyche. Structuralists like Claude Lévi-Strauss ventured further, exploring how deep patterns hide beneath cultural phenomena, myths, and language. Each approach suggests we can look past the “accidents” of appearance or context and find a hidden unity. Picasso’s final bull drawing feels archetypal: it is “bull-ness” without the individuality of any particular bull.

Category Theory, a branch of mathematics often called the “mathematics of mathematics,” explores objects by their relationships (morphisms) rather than their isolated natures. For instance, the “object” that underlies square, cube, and tesseract can be treated as a fundamental shape that appears differently in 2D, 3D, 4D, etc. Each shape is a manifestation or transformation of this more abstract entity.

Bohm’s Implicate Order: A Deeper Layer of Reality

Now back to our physicist David Bohm. He proposed that the visible, tangible world we experience is the explicate order— manifestation of a more fundamental, implicate order. Bohm argued that everything we see in the explicate (unfolded) world is rooted at a deeper level, hidden (enfolded) into a dynamic, interconnected layer of the world. This implicate order contains the idea that will unfold in the thing in the explicate order.

Monads: The Ultimate Building Blocks?

Gottfried Wilhelm Leibniz (1646–1716) introduced the idea of monads—fundamental, indivisible units of reality that mirror the entire universe in itself. Modern thinkers sometimes see these monads as kernels of information, microcosms of the entire cosmic story. Whether interpreted literally or metaphorically, the monad suggests that everything is enfolded within each part. If information precedes form, one could say that each monad encodes a perspective on the universal whole.

One limitation of these discussions on the “essence” or “idea” behind things is that if we treat them too superficially, we risk slipping into a kind of hyper-determinism—as though each idea were merely a prefabricated template waiting to be printed into physical reality. This can overlook the creative variety and emergent processes that arise when ideas interact with the complex physics and unfolding of the actual world. While deep structures may underlie our reality, they do not necessitate rigid predictions of what will come to be. Instead, they’re more like guiding frameworks that can evolve and interact in infinitely varied ways—ever open to being reinterpreted, repurposed, or transformed.

So…What Is a Thing Before It Becomes a Thing?

Returning to our original question: What exist before a thing becomes a thing? There are many ways to start understanding the problem:

Phenomenology (Husserl) emphasizes the eidetic essence—that which remains when all contingencies are stripped away.
Archetypal and Structural viewpoints see a universal pattern behind each individual manifestation.
Category Theory speaks of transformations and relationships that point back to an abstract “object” existing in different forms.
Bohm’s Implicate Order suggests that the divisions of space and time themselves are secondary; deeper reality is an unbroken whole from which forms “unfold.”
Monads (Leibniz) evoke the possibility of minimal “information-points” that collectively generate our reality.

Putting all these threads together opens a world behind our world.

A deeper “idea” precedes each particular “thing.”

This idea can manifest (unfold) in myriad ways, depending on context, perspective, or dimension.

Whether we call it - “information,” “archetype,” “monad,” or “implicate structure” - it initiates, at least partially, the blueprint for how reality shapes itself into the explicit forms we recognize.

What unites these perspectives is the conviction that the world of distinct objects we see is not the deepest layer of reality. Instead, something more subtle—a universal “idea” or wholeness—lies beneath. The square, the cube, and the tesseract, like Picasso’s bull, are all different ways this deeper essence makes itself visible.

A Final Reflection

In the end, the story of Picasso’s bull resonates with Husserl’s call to peel away the layers until we glimpse an essence that makes up the inherent individuality of something. However we call it, the idea is the same: something is there before we name it, before the object stands out against the background of the world. As a last cosmological parallel, this inquiry resonates with one of our core questions at the Science and Philosophy Institute: What was there before the origin of the universe, before the Big Bang? I am still working through my own reflections on the idea behind the thing. Does the idea necessarily point to something simpler and, paradoxically, more universal? Can this process help us better understand how things come into being? How can we think of essence and idea in a non-deterministic universe?

This journey from archetypes to implicate order, in whatever discipline we touch—physics, art, philosophy—is a reminder that behind every apparent “thing,” there is a deeper realm of relationships, structures, and potential—an infinite canvas from which reality’s forms emerge.